MECÂNCIA GENERALIZADA GRACELI DE INTERAÇÕES E TRANSFORMAÇÕES.

LEI -

TODA INTERAÇÃO LEVA  A TRANSFORMAÇÕES, E VICE-VERSA.

INTERAÇÕES COMO E EM:

NAS INTERAÇÕES DAS FORÇAS FUNDAMENTIAS.

INTERAÇÕES DE SPIN - ÓRBITA.

ESTRUTURA - TEMPERATURA.

DISTRIBUIÇÃO ELETRÔNICA - NÍVEIS DE ENERGIA - BANDAS.

ELÉTRONS - FÓNOS.

ELÉTRONS - ELÉTRONS.

ESTADO QUÂNTICO - NÚMERO QUÃNTICO.

ENTROPIA -TEMPERATURA - MOVIMENTO BROWNIANO - CAMINHOS DE PARTÍCIULAS.

CATEGORIA - DIMENSÕES - FENÔMENOS [NO SISTEMA SDCTIE GRACELI].

ENTROPIA - ENTALPIA. ETC.

VEJAMOS AS INTERAÇÕES DE CAMPOS.

E EM RELAÇÃO AO SISTEMA  DE MECÂNICA GENERALIZADO GRACELI.

   eletromagnetismo quântico químico relativístico Graceli.

MECÂNICA DO SISTEMA DIMENSIONAL GRACELI.

ONDE A MAIORIA DOS FENÔMENOS FÍSICOS [EM TODAS AS ÁREAS] VARIAM CONFORME O SISTEMA DIMENSIONAL GRACELI.

SENDO ELE;

      EQUAÇÃO GERAL DE GRACELI.[quantização de Graceli].

  G ψ = E ψ = IGFF   E [tG+].... ..  =

G ψ = E ψ = IGFF  E [tG+]ψ ω /c] =   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   [ q G*]ψ μ / h/c ψ(x, t)  [x  t ]..

[ q [tG*] ==G ψ = E ψ = IGFF   E [tG+].... .. 

SISTEMA GRACELI DE:

 TENSOR [tG+] GRACELI = IGFF + SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA., POTENCIAL DE ENERGIA, POTENCIAL QUÍMICO,  SISTEMA GRACELI DO INFINITO DIMENSIONAL.

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI. 

[ q [tG*] = energia quântica Graceli.

Força fundamental - INTERAÇÕES GRACELI IG =

IGFF = INTERAÇÕES GRACELI -  Força fundamental.

 T = TEMPERATURA.

PERMEABILIDADE MAGNÉTICA .

INTERAÇÃO SPINS ÓRBITA.

MOMENTUM MAGNÉTICO.

DISTRIBUIÇÃO ELETRÔNICA DOS ELEMENTOS QUÍMICOS.

NÍVEIS E SUBNIVEIS DE ENEREGIA.

BANDAS DE ENERGIAS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [1]

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =  E [tG+].... ..  [2]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [-1]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =  E [tG+].... ..  [-1]

RELATIVIDADE DAS FORÇAS FUNDAMENTAIS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. / c .

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =  E [tG+].... ../ c .

Exergia é o trabalho máximo que pode ser obtido através do processo mais adequado de um sistema que se encontre em um estado inicial até que atinja o estado final, caracterizado pelo equilíbrio termodinâmico com o ambiente. Essa grandeza pode ser definida também como potencial máximo de trabalho de uma substância ou trabalho mínimo para fazer o sistema sair do estado morto.

O termo foi definido por Zoran Rant, chamando de “exergia” a parte da energia disponível para produzir trabalho útil e de “anergia” a quantidade de energia não disponível para o mesmo fim. Ao contrário da energia, a exergia não pode ser conservada, já que é destruída por processos irreversíveis em razão do aumento de entropia.

A exergia se torna uma propriedade de combinação entre o sistema e o ambiente, uma vez definida como o trabalho máximo que um sistema pode desenvolver para chegar ao equilíbrio térmico, mecânico e químico com o ambiente. Dessa forma, uma vez que se define o ambiente, a exergia pode ser considerada propriedade do sistema.

Historicamente, exergia foi o primeiro conceito a começar a ser proposta na termodinâmica, quando Carnot afirmou que “para transformar calor em energia cinética, utiliza-se uma máquina térmica, porém esta não é 100% eficiente na conversão”. A partir de seus trabalhos, a Segunda Lei da Termodinâmica foi definida. Após Carnot, outro físico de grande importância na definição de exergia foi Gibbs, que conceituou energia disponível como a propriedade que mede a capacidade de causar mudanças devido ao desequilíbrio com o ambiente de certa substância.

Tipos de Exergia

Matematicamente, a exergia pode ser representada pela letra B, e é definida pela soma dos quatro tipos de exergia existentes: potencial, cinética, física e química.

${\displaystyle B=B_{P}+B_{C}+B_{F}+B_{Q}}$ /  G ψ = E ψ = IGFF   E [tG+].... .. 

Exergia Potencial

A energia potencial, por ser uma forma de energia mecânica, se transforma completamente em trabalho e, portanto, é igual a energia potencial.

${\displaystyle B_{P}=m.g.h}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

Onde m = massa, h = elevação e g = 9,81 m/s² (ao nível do mar).

Exergia Cinética

Assim como a energia potencial, a energia cinética é uma forma de energia mecânica. Dessa forma, a exergia cinética é igual a energia cinética.

${\displaystyle B_{C}={\frac {mv^{2}}{2}}~}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

Onde m = massa e v = velocidade.

Exergia Física

Também pode ser chamada de exergia termomecânica, e é definida como o trabalho máximo obtido quando uma dada substância é levada a atingir o equilíbrio termomecânico com o ambiente.

${\displaystyle B_{F}=\Delta U+P_{o}\Delta V-T_{o}\Delta S}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

Onde U = energia cinética, P = pressão, V = volume, T = temperatura e S = entropia.

Exergia Química

Exergia química é a máxima quantidade de trabalho que é obtida quando uma dada substância é trazida do estado natural por processos envolvendo transferência de calor e troca de matéria com o ambiente.

${\displaystyle B_{Q}=Q.(1-{\frac {To}{T}}~)}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

Onde Q = calor e T = temperatura.

Em física, o fator de Boltzman é um fator de ponderação que determina a probabilidade relativa de um estado ${\displaystyle i}$, num sistema com múltiplos estados em equilíbrio termodinâmico a temperatura ${\displaystyle T}$.^[1]

${\displaystyle e^{-{\frac {E_{i}}{k_{B}\,T}}}}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

Onde ${\displaystyle k_{B}}$ é a constante de Boltzmann, e ${\displaystyle E_{i}}$ é a energia do estado ${\displaystyle i}$. A relação das probabilidades dos estados é dada pela relação (quociente) de seus fatores de Boltzmann.

O fator de Boltzmann não é em si mesmo uma probabilidade, já que não está normalizada. Para normalizar o fator de Boltzmann e converter-lo numa probabilidade, deve-se dividi-lo pela soma ${\displaystyle Z}$ dos fatores de Boltzmann de todos os estados possíveis do sistema, o qual se denomina função de partição. Desta forma se obtem a distribuição de Boltzmann.

A partir do fator de Boltzmann é possível desenvolver a estatística de Maxwell-Boltzmann, a estatística de Bose-Einstein e a estatística de Fermi-Dirac que regem as partículas clássicas como também os bósons e férmions na mecânica quântica, respectivamente.

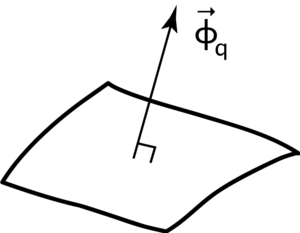
Fluxo de calor, fluxo termal ou fluxo térmico é a taxa de energia térmica (calor) transferida de uma dada superfície. Pode ser quantificado por seu valor transferido por unidade de área em uma unidade de tempo. Em unidades do Sistema Internacional (SI), é medido em [W·m⁻²].^[1] Possui tanto uma direção quanto uma magnitude, sendo portanto, um vetor, uma grandeza vetorial.^[2] Para definir a densidade de fluxo de calor em um certo ponto no espaço, toma-se o caso limite onde a superfície torna-se infinitesimalmente pequena.

Densidade de fluxo de calor ${\displaystyle {\overrightarrow {\phi _{q}}}}$ através de uma superfície.

A densidade de fluxo de calor é frequentemente notada ${\displaystyle {\overrightarrow {\phi _{q}}}}$, o subescrito q especificando fluxo de calor, diferenciando-se de fluxo de massa ou momento. A lei de Fourier é uma importante aplicação destes conceitos.

Medição do fluxo de calor

Ver artigo principal: Sensor de fluxo de calor

A medição do fluxo de calor é na maioria das vezes feita medindo a diferença de temperatura ao longo de um pedaço de material com condutividade térmica conhecida. Este método é análogo ao uso de um padrão de resistência elétrica para medir uma corrente elétrica, em que se mede a queda de voltagem em um resistor conhecido.

Relevância para ciência e engenharia

Uma das ferramentas de um cientista ou engenheiro é o balanço de energia. Tal balanço pode ser realizado para qualquer sistema físico, de reatores químicos a organismos vivos, e geralmente toma a seguinte forma

${\displaystyle {\big .}{\frac {\partial E_{\mathrm {e} }}{\partial t}}-{\frac {\partial E_{\mathrm {s} }}{\partial t}}-{\frac {\partial E_{\mathrm {a} }}{\partial t}}=0}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

onde os três termos ${\displaystyle {\big .}{\frac {\partial E}{\partial t}}}$ representam a taxa no tempo da quantidade total de energia entrando, a quantidade total de energia saindo e a quantidade total de energia acumulada, respectivamente.

No entanto, se o único meio pelo qual o sistema troca energia com suas proximidades é através da transferência de calor, o fluxo de calor pode ser usado para calcular o balanço de energia, já que

${\displaystyle {\big .}{\frac {\partial E_{\mathrm {e} }}{\partial t}}-{\frac {\partial E_{\mathrm {s} }}{\partial t}}=\oint _{S}{\overrightarrow {\phi _{q}}}\cdot \,{\overrightarrow {dS}}}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

onde integra-se a densidade de fluxo de calor ${\displaystyle {\overrightarrow {\phi _{q}}}}$ sobre a superfície ${\displaystyle S}$ do sistema.

Em aplicações do mundo real não é possível conhecer a densidade do fluxo de calor exato em cada ponto da superfície, mas esquemas de aproximação podem ser usada para calcular a integral, como por exemplo a integração de Monte Carlo.

Fluxo de calor crítico descreve o limite térmico de um fenômeno onde uma mudança de fase ocorre durante o aquecimento (tal como bolhas formando-se sobre uma superfície de metal usada para aquecer água),a qual subitamente diminui a eficiência da transferência de calor, então causando superaquecimento localizado da superfície de aquecimento.

O fluxo de calor crítico para ignição é a mais baixa carga térmica por unidade de área capaz de iniciar uma reação de combustão em um dado material (tanto uma ignição com chama como "brasa").

Descrição

Quando líquido refrigerante sofre uma mudança de fase devido à absorção de calor de uma superfície sólida aquecida, uma taxa de transferência mais alta ocorre. A transferência de calor mais eficiente a partir da superfície aquecida (na form de calor de vaporização mais calor sensível) e os movimentos de bolhas (turbulência e convecção conduzida por bolhas) leva à rápida mistura do fluido. Portanto, a transferência de calor por ebulição desempenha um importante papel nos processos de transferência de calor industrial tais como a transferência macroscópica em trocadores em termoelétricas nucleares e baseadas em combustíveis fósseis, e em dispositivos de transferência de calor microscópicos tais como tubos and microcanais para resfriamento de circuitos integrados ("chips") eletrônicos.

O uso da ebulição é limitado por uma condição chamada fluxo de calor crítico (FCC), o qual é também chamado uma "crise de ebulição" ou "partida da ebulição nucleada (PEN). O mais sério problema é que a limitação da ebulição pode ser diretamente relacionada à burnout física dos materials de uma superfície aquecida devido à repentinamente ineficiente transferência de calor através de um filme de vapor formado através da superfície resultante da substituição de líquido por vapor adjacente à superfície aquecida.

Consequentemente, a ocorrência de FCC é acompanhada por um aumento exagerado da temperatura da superfície para um sistema de superfície de fluxo de calor controlado. Caso contrário, uma diminuição excessiva da taxa de transferência de calor ocorre para um sistema de superfície com temperatura controlada. Isso pode ser explicado com a lei de Newton do resfriamento:

${\displaystyle q=h(T_{w}-T_{f})\,}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

onde ${\displaystyle q}$ representa o fluxo de calor, ${\displaystyle h}$ representa o coeficiente de transferência térmica, ${\displaystyle T_{w}}$ representa temperatura da parede e ${\displaystyle T_{f}}$ representa a temperatura do fluido. Se ${\displaystyle h}$ diminui significativamente devido à ocorrência da condição de FCC, ${\displaystyle T_{w}}$ irá aumentar por ${\displaystyle q}$ e ${\displaystyle T_{f}}$ fixos enquanto ${\displaystyle q}$ irá diminuir por ${\displaystyle \Delta T}$ fixa.

Uma função de estado é uma função que descreve uma relação entre duas ou mais variáveis de estado que definem o estado de um sistema termodinâmico. Designa também qualquer variável de estado assumida dependente daquelas escolhidas para definirem-se os estados do sistema e por tal tratadas como independentes.

Definição

Em termodinâmica, as variáveis de estado ou variáveis termodinâmicas são as grandezas físicas termodinâmicas utilizadas na definição e descrição do estado de um sistema termodinâmico.

Algumas das variáveis de estado, comuns a todos os sistemas termodinâmicos massivos, incluso os mais simples, são:

massa (m) ; quantidade de matéria (n) ; Pressão (P) ; Temperatura (T) ; Volume (V) ; Energia interna (U) e Entropia (S).

Há ainda outras, não menos importantes, tais como:

Entalpia (H) ; Energia livre de Helmholtz (A); Energia livre de Gibbs (G); Magnetização (${\displaystyle {\vec {M}}}$) ; etc.

Um estado de um sistema é descrito por um conjunto específicos de valores de suas variáveis de estado. A definição de "estado" do sistema - e mesmo das variáveis de estado - assume em princípio o sistema em equilíbrio termodinâmico.

Um dado sistema termodinâmico altera o seu estado de equilíbrio em virtude de alterações nas interações que estabelece com a sua fronteira ou mesmo vizinhança. Ao fazê-lo, o processo desencadeado pode dar-se e usualmente se dá de forma abrupta o suficiente para que não se possa definir estado de equilíbrio durante a transição entre os assumidos estados de equilíbrio inicial e final. Poucos são os casos onde os processos - então nomeados processos quasi-estáticos - dão-se de forma adequada o suficiente para que se possa corretamente descrevê-los via uma sequência de incontáveis transições diferenciais entre estados de equilíbrio imediatamente adjacentes, ou seja, entre estados quasi-idênticos, de forma que o sistema possa sempre ser assumido estar em equilíbrio termodinâmico em qualquer instante durante a transição.

O conjunto de valores das variáveis de estado define o estado do sistema apenas quando esse encontra-se no equilíbrio termodinâmico, e tais variáveis não podem - ao menos sem considerações muito específicas - ser usadas para descrever a evolução temporal do sistema na grande maioria dos processos termodinâmicos onde, durante a transição de um estado de equilíbrio a outro, o sistema não está em equilíbrio (muitas das variáveis de estado não são sequer definidas em tal situação). Tal descrição é corretamente possível apenas nos processos quasi-estáticos.

Independente da forma como se dá o processo que culmina por levar o sistema de um dado estado a outro qualquer, uma vez comparados os valores das variáveis de estado nos diversos estados de equilíbrio possíveis para o sistema (usualmente mas não necessariamente um sistema fechado), verifica-se contudo que, em qualquer estado, há vínculos e restrições de natureza física conectando os diversos valores possíveis das variáveis de estado. Igualmente satisfeitos em qualquer estado do sistema, são tais vínculos que, nos processos termodinâmicos, não permitem que os valores das variáveis de estado se alterem de forma indiscriminada ou mesmo de forma completamente independente das demais, mesmo que o processo entre os estados seja em essência um processo caótico e de não equilíbrio.

As relações de dependência entre as variáveis - as funções de estado, traduzidas matematicamente na forma de equações de estado - são relações que conectam os possíveis valores de um dado subconjunto de variáveis de estado de um sistema. Dá-se também o nome de "função de estado" às variáveis de estado que são assumidas dependentes de outras - geralmente daquelas escolhidas para definir-se o estado. Assim, a energia interna U de um gás ideal é dita ser uma "função de estado; sendo as variáveis independentes - as que definem o estado no estudo de tais gases - usualmente escolhidas como sendo a temperatura T, a pressão P e o volume V do gás.

É nesses termos e com base no antes exposto que se diz: A variação de uma função de estado depende apenas do estado final e do estado inicial do sistema.

Uma função de estado estabelece relações entre um determinado número de variáveis de estado, mas não necessariamente entre todas simultaneamente, havendo assim várias equações de estado possíveis para um sistema. Uma função de estado usualmente não encerra em si todas as propriedades físicas do sistema, e não é assim capaz, ao menos sozinha, de descrevê-lo completamente. Precisa-se usualmente de um conjunto mínimo de equações de estado independentes para fazê-lo.

É possível contudo escrever-se uma única equação - nomeada equação fundamental - que encerra em si todas as propriedades físicas do sistema. Essa equação descreve, sozinha, todo o sistema, e dela é possível extrair-se todas as equações de estado desejadas. Para fazê-lo basta utilizar o formalismo termodinâmico associado.

Exemplo - Gás monoatômico ideal

Considere um sistema definido por uma certa massa de gás ideal monoatômico. A análise de tal sistema revela que, para ele, há as seguintes equações de estado:

${\displaystyle PV=nRT}$ (relação de Clapeyron)

Nas expressões anteriores, n representa a quantidade de matéria do sistema, em mols, e R é a constante dos gases ideais.

As partículas de um gás monoatômico só possuem movimentos de translação e, como se trata de um gás ideal, não interagem entre si. Assim, classicamente, a energia interna deste gás é dependente apenas da energia cinética das partículas, energia que por sua vez liga-se diretamente ao conceito de temperatura do sistema. Logo, nesse caso, a energia interna é função exclusiva da temperatura. Basta saber-se a temperatura de uma amostra de gás ideal em equilíbrio termodinâmico que pode-se, então, determinar sua energia interna.

A relação para a energia interna do gás em função da temperatura acima define uma função de estado. Observe que a energia interna depende da temperatura contudo independe de como o sistema chegou à essa temperatura. Qualquer que seja o processo a qual se submeta o sistema, provido que esse regresse à mesma inicial temperatura T, ter-se-á uma variação nula de sua energia interna.^[1]

Observe contudo que pode-se combinar as duas equações acima para se gerar outra equação de estado, uma que envolva a energia interna, a pressão e o volume:

${\displaystyle U={\frac {3}{2}}PV}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

Para um mesmo valor de temperatura e por conseguinte para uma mesma energia interna, há diversos estados possíveis do sistema, cada qual com uma pressão e um volume diferentes.

Embora possam-se cogitar outras equações de estado, nenhuma delas, sozinha, encerram em si todas as informações físicas acerca do sistema.

Ao contrário, uma equação que vincule a energia interna U do gás ideal à sua entropia S, ao seu número de partículas N e ao seu volume V encerrará em si própria todas as informações físicas pertinentes ao sistema assim definido, e constitui assim uma equação fundamental de tal sistema. A título de curiosidade, a equação fundamental para um sistema composto por N partículas de um gás ideal confinados em um volume V e com energia interna U é, na representação da energia, com ${\displaystyle k_{B}}$ representando a constante de Boltzmann e c uma constante adequadamente escolhida:

${\displaystyle U_{(S,V,N)}=N\left({\frac {N}{V}}\right)^{\frac {2}{3}}e^{{\frac {2}{3}}\left({\frac {S}{Nk_{B}}}-c\right)}}$ /

  G ψ = E ψ = IGFF   E [tG+].... .. 

^[2] 

Através da transformada de Legendre é possível reescrever-se à equação acima, obtendo-se assim várias outras equações fundamentais, cada qual encerrando sozinha todas as informações físicas acerca do sistema em consideração.